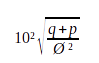Fonction δ de Ulmenos
La fonction δ de Ulmenos est une fonction permettant de déduire la densité atmosphérique d’une planètes selon sa pression atmosphérique et la grandeur de son atmosphère.
Histoire
Découverte en -28 av. Castulus par le scientifique otsin Klimen Ulmenos par l’observation de l’atmosphère, cette fonction est désormais très utilisée dans les milieux scientifiques. Klimen Ulmenos a observé l’atmosphère et en a déduit une relation entre la pression atmosphérique et la taille de l’atmosphère. Après un certain temps de réflexion, il a déduit la fonction qui a posé la base des théories magicoplanétaires.
Énoncé
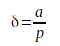
Où a désigne la taille de l’atmosphère en km et p la pression atmosphérique au niveau de la mer en kPa.
Le résultat s’exprime en Uo.
Exemples d’Application
La Terre a pour pression atmosphérique 101 325 Pa au niveau de la mer et la taille de son atmosphère est de 800 km.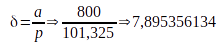
La Terre a donc pour densité atmosphérique 7,9 Uo.
Cast a pour pression atmosphérique 120 627 Pa au niveau de la mer et la taille de son atmosphère est de 200 km.
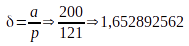
Cast a donc pour densité atmosphérique 1,65 Uo.
Utilisation
La fonction δ de Ulmenos est utilisée par exemple dans le principe d’Ønstein.
Principe d’Ønstein
Le Principe d’Ønstein est un principe permettant de déduire la quantité magique d’une planète et de la mesurer.
Histoire
Miklor Ernelor Ønstein a découvert le principe portant son nom en 658 ap. Castulus. Ce savant dombélien passionné d’astronomie a un jour réalisé que, chaque planètes disposant d’un potentiel magique comme il a été démontré par le Théorème de Klalos, il était sûrement possible de calculer ce potentiel magique par de simples observations astronomiques. Se basant donc sur sa planète, Cast, il a effectué ce principe et a reçu en récompense un domaine privé.
Enoncé
Celon les matériaux du noyaux, de la densité atmosphérique et le diamètre d’une planète, il est possible de déduire son potentiel magique.
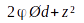
Où z représente le numéro atomique du matériau le plus présent dans le noyau, Ø le diamètre de la planète en km et d la moyenne de la densité atmosphérique calculée par la fonction δ de Ulmenos.
Le résultat est exprimé en Ø, soit en Ønstein et représente le potentiel magique d’une planète. C’est toujours un Entier Naturel.
Le principe ne peut être exact à cause de la perdition progressive du potentiel magique lors de surutilisation
Exemples d’Application
La Terre a une densité atmosphérique de 7,9 Uo, un diamètre de 12 742 km et d’un numéro atomique de 26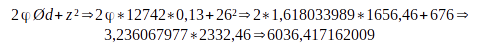
La Terre a donc un potentiel magique de 6036 Ø (nb. aujourd’hui il est tombé à 1529 Ø).
Cast a une densité atmosphérique de 1.658 Uo, un diamètre de 10 251 km et d’un numéro atomique de 26.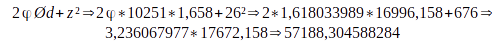
Cast a donc un potentiel magique de 57188 Ø (nb. aujourd’hui il est tombé à 56 125 Ø)
Utilisation
Ce principe est utilisé dans le calcul du QMP
QMP
Le QMP, ou Quotient Magique Planétaire est une formule mathématique permettant de calculer la puissance magique d’une planète.
Histoire
Le QMP a été inventé en 714 ap. Castulus par un savant otsin du nom de Iekor Olsopranik. Il cherchait alors à prévoir la capacité magique d’éventuelles nouvelles planètes. Il a donc mis au point une formule qui donne un nombre qui représente le QMP de la planète. Il a été ensuite récompensé par le congrès scientifique des pays de l’Otso par son admission à l’École de Kelneos, école dont il a toujours voulu faire partie.
Enoncé
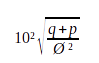
Où Ø est le diamètre de la planète en km, q la quantité magique calculée par le Principe d’Ønstein et p le pourcentage de personnes ayant accès à la magie (exprimé en nombre réel et non pas en pourcentage).
Le QMP est exprimé comme un nombre avec trois chiffres après la virgule.
Exemples d’Application
La planète Terre a pour rayon 12 742 km, une quantité magique de 1529 Ø et 0% de la population a accès à la magie.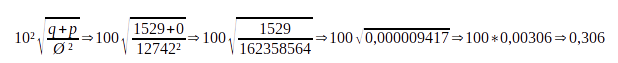
Donc la Terre a un QMP de 0,306.
La planète Cast a pour rayon 10 251 km, une quantité magique de 56 125 Ø et 98% de la population a accès à la magie.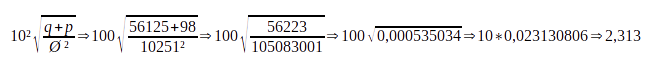
Donc Cast a un QMP de 2,313
![]()